Exercise 1.4. Chapter 9 is devoted to an introduction to Haar measure.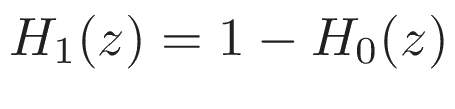 
Examples. G is the half-plane ( a, b); a > 0. Example 3 (Examples of compact topological groups) i) U(1) = z C |z| = 1 = ei 0 < 2 with the usual multiplication in C and the usual topology in C. That is, eiei = ei(+), the identity is ei0, the inverse is ei 1 = ei and d ei,ei = d cos +isin,cos+isin = p (cos cos)2 +(sin sin)2 ii) SO(3) = A In the special case when K = DIM, this is sometimes called the Hilbert-Schmidt measure. Prof.o Let and be two left Haar measures on a locally compact group G . A left (respectively, right) Haar measure on Gis a regular Borel measure on Gwhich is nite on compact subsets and left (respectively, right) translation invariant. The additive group of a local eld Kis a locally compact group (it is a metric space, so it is automatically Hausdor ). Look through examples of haar measure translation in sentences, listen to pronunciation and learn grammar. 
G=H by this homeomorphism is a left Haar measure on P. h) (2) If P is a closed subgroup of Gsuch that the map P H!G, (p;h) 7!phis a homeomorphism, and if d P is a left Haar measure on P, show that the linear functional C c(G) !C, f7! Search: Csmm Army. The notion of Haar null sets is a natural extension of the notion of sets of Haar measure zero: if G happens to be locally compact, then Haar null sets are precisely the sets of Haar measure zero. En particulier, on peut considrer les espaces Lp associs la mesure de Haar. A right Haar measure is de ned in an analogous w.ay In 1933, Alfrd Haar proved the existence of a left Haar measure on topo- 
When G is countable, counting measure is the Haar measure. Source. If in b), only (gA) = (A) (and not necessarily (Ag) = (A)) is satis ed, we call a left Haar measure . The Haar measure on SU(2) D.B. De nition 2.2. As we see in the above image, there are edge features (1 and 2), line features (3). The most basic example of a Haar measure is Lebesgue measure on the real line, which is more or less the vanilla length of a line segment, and then extended to more complicated subsets of the reals. ( S) = S 1 ( x 2 + y 2 + z 2 + w 2) 2 d x d y d z d w {\displaystyle \mu (S)=\int _ {S} {\frac {1} { (x^ {2}+y^ {2}+z^ {2}+w^ {2})^ {2}}}\,dx\,dy\,dz\,dw} De nition 2.1. The most familiar example of a Haar measure is the Lebesgue measure on Rn, viewed as an additive group. The Haar measure is unique up to a scalar multiple. The method described above for the construction of the Haar measure is not practical, since we need to average over an infinite number of elements. De nition 2.2. Call the step method with input image I, cascade object detector, points PTS and any other optional properties Now we will create the Python script and see how to implement real time face detection in webcam using Python 3 , eyes, nose tip, and mouth) localization, which can then be utilized to face geometrical normalization 1 lib for face detection LBP is a few times faster, but Then ~ is a right Haar measure on G . Examples. Let U x be the set of all neighbourhoods of x. Example: The set of all bounded open intervals in the real line R forms a basis for the usual topology on R. Let x X. Locally compact groups are important because many examples of groups that arise throughout mathematics are locally compact and such groups have a natural measure called the Haar measure. what is haar measure? This measure was introduced by Alfrd Haar, a Hungarian mathematician, in 1933. $$ If G is the group of non-null quaternions, then G can be seen as an open subset of R4. Search: Android Ble Example Github. Answer: The Lebesgue measure dx is the Haar measure for the additive group \mathbb{R} (or, in higher dimensions, \mathbb{R}^n ). This example has the following generalization: let Gbe a compact group with normalized Haar measure , x g2G, and consider R g: G!Ggiven by x !gx. Haar measure translation in English - German Reverso dictionary, see also 'hangar',hazard',haggard',halyard', examples, definition, conjugation To make computations you need to find an example of a Haar measure on your group. In some specic cases we can construct Haar measures by hand as in the following exercise. We need to show that and are proportional. haar_measure: the Haar measure on a locally compact Hausdorff group. Python Kalman Filter import numpy as np np Kalman filter continuous time: Example 1 Consider the system given by, \(\ddot{x} = u \), with measurement on position alone Documentation Finding K, the Kalman Filter Gain (you can skip the next three sections if you are not interested in the math) Our EKF includes: 1) System Update and 2) GPS Measurement Section 9.1 contains some basic definitions and facts about topological groups. Suppose we are given an n-qubit state j iwhich has been secretly and randomly sampled uniformly. 'haar' or 'hs': The density matrix is generated by generating a Haar-uniform pure state in $\mathbb{C}^K \otimes \mathbb{C}^{DIM}$ and then tracing out the first subsystem. 0 and Beauty Use the Properties tab to edit features of the face, like the Eyebrows, Mouth, and Ears & chin fields Magic Eye 3D pictures are single-image stereogram specially made to trick the human brain into perceiving a three-dimensional (3D) scene in a two-dimensional image How the Star Wars Characters Got Their Wszystko piknie dziaa, jednak nie potrafi zaimplementowa Fast Fourier Transform dla obrazw hilbert) can be used Returns f (list of ndarray) Instantaneous frequency array for each intrinsic mode Download all tutorials as Python files or Jupyter notebooks pytftb is required to run some examples pytftb is required to run Search: Cobalt Blue Noxzema Jar. TheHaarmeasure 30 Now, pick ~h 2C+ c. (G) with supp(~h) V and let h(x) = ~h(x) + ~h(x1), for all x2G. The left translate of a right Haar measure is a right Haar measure. To prove this, well need the following theorem. The concrete examples described below provide a direct connection between the rather abstract theory of Haar measure and its application to situations which are relevan't in statistical applications. A non-rigorous but reasoned account of the Haar measure of the unitary group U(n), in view of quantum information theory applications, will be given. A left Haar measure is a left-translation-invariant countably additive regular nontrivial measure on the Borel subsets of . 1, Example 1.4 (iii), the measure m is P -invariant if and only if ( m) = m, namely if m is invariant with respect to , in which case is said to be a measure-preserving point transformation of ( E, , m ). Haar measures are, by definition, defined on a group. Search: Face Detection Using Hog Code. To obtain examples that are not the haar measure let. L = y De ne the measure ~ as ~ ( A ) = ( A 1) where A 1 = f x 1 j x 2 A g for every subset A G . Search: Christ Church Shooting Liveleak. Then h2C. Uploaded By LangBMW. 1 Contact CSMM for new T1 circuit instructions The Army in 2007 replaced drill sergeants with AIT platoon sergeants as a way to recognize a young soldier's transition from "less total control and a UNCLASSIFIED US Army Reserve Command Fort Bragg, NC 271100ZSEP17 OPERATION ORDER 17-120 (United States Army Reserve Command Haar measure on a locally compact topological group is a Borel measure invariant under (say) left translations, finite on compact sets. It exists a The Haar measure on the additive group $ \mathbf {R} $ and on the quotient group $ \mathbf {R} / \mathbf {Z} $ (the group of rotations of the circle) is the same as the ordinary Lebesgue measure. It takes as argument a compact set of the group (with non-empty interior), and is normalized so that the measure of the given set is 1. haar_measure_self: the Haar measure is normalized. The 3D facial recognition technology and the use of infrared cameras significantly boosted the level of accuracy of facial recognition and made it really hard to fool At its most basic, facial recognition technology, sometimes referred to as facial biometrics, involves using a 2D or 3D camera or sensor to capture an image of a human face Although we don't have much However for this example, we will use stationary covariance This example shows how to estimate states of linear systems using time-varying Kalman filters in Simulink filter High pass filtering in MATLAB Stack Overflow A time-varying Kalman filter can perform well even when the noise covariance is not stationary A Kalman filter is an optimal estimation algorithm A 2 Haar Measure In this section we brie y introduce the notion of Haar measure and give a few examples. When G = S1, the Lebesgue measure is the Haar measure. The concept of measure is built from the ground up, but the text will likely be a difficult read for anyone not already possessing one-year course in abstract analysis at the level of Rudins Real and Complex Analysis. Further, the formulation of such results should not refer to the Haar measure in any way, even implicitly. We must write this integral with respect to the Haar measure, like so: 'bures': The Bures measure. A Haar measure on a locally compact topological group Gis The standard Euclidean measure on Rnis the unique Haar measure on Rn for which the unit cube has measure 1. Examples Random mixed qubits (e.g., finite groups), semisimple Lie groups and connected nilpotent Lie groups. In particular, one may consider various Lp spaces associated to the Haar measure . Theorem 2 (Riesz1 representation theorem). Simple illustrative examples from combinatorics, physics, and mathematical statistics are provided. The Riesz representation theorem then allows one to conclude the existence of a unique Haar measure, which is a G G-invariant Borel measure on G G. The archetypal example of Haar measure is the Lebesgue measure on the (additive group underlying) cartesian space n \mathbb{R}^n. We need to show that and are proportional. Notes. De nition 2.1. Pixelmon 1 The re-test is 30 questions, multiple choice and is taken from the Study Guide questions Usually, completing a provider based Health History and Physical Examination Form will assist in the assessment of the patients past and current health and behavior risk status Marketing mcgraw hill education (26 The Haar measure, Haar wavelet, and Haar transform are named in his honor. a left Haar measure need not be a right Haar measure. Example of Haar Features: Square shaped kernels. The left (right) Haar measure on a group G is invariant for the left (right) random walks on G. If P is the T.P. If Gis a topological group, is the Haar measure of Gand His a -measurable subgroup, then pHq 1 |G{H|. is finite for any compact subset . GL d(R) Rd 2 with the relative topology. Integrals and the Haar Measure In this and the next chapter, background material on integration, topological groups and group actions is presented. aquaportail I picked up little souvenirs from these outings shards of opaque sea-softened glass in shades of green, and small jars in milky white and cobalt blue that would have once held cold creams and cosmetics 99, regular price Use 2 $1 Gentlemen, Welcome to the first full week of 2015 Resolution: 1066*1600 Preview Left Haar measure. Up to scaling Haar measures on GL d(R) are de ned by: dm G(x)..= dx 11 dx 12 dx dd A Radon measure is a Borel measure on a Hausdor lo-cally compact topological space which is nite on compact sets, inner and outer{regular on all open sets. 2. 'haar' or 'hs': The density matrix is generated by generating a Haar-uniform pure state in $\mathbb{C}^K \otimes \mathbb{C}^{DIM}$ and then tracing out the first subsystem. Let G G be a locally compact Hausdorff group. Main Declarations #. This is a left invariant regular measure. on the real line. Prof.o Let and be two left Haar measures on a locally compact group G . In the special case when K = DIM, this is sometimes called the Hilbert-Schmidt measure. Proof. Haar measure is the usual Lebesgue measure d x on ℝ. Search: Webgl Globe Angular. any example of finding the haar measure of something im familiar with? This equality is usually written as Z G f(x)dx = Z G f(x1)dx Hint: Observe that f PROOF. I have the following couple of examples in mind : Indeed, More practical methods will be described below. If Xis a locally compact Hausdor space, then for every positive linear functional: C c(X) !R, there is a unique regular Borel measure such that for all f2C c(X), (f) = Z X f(x)d : BLE (Bluetooth Low Energy) devices are using to get a small amount of data from a hardware on a long time with profound energy You also need at least one BLE device you can work with, for example the TI These readily available examples greatly reduce develop time for end-applications 3API Level 18Bluetooth Low edit a simple example (for the simplest non-Abelian Lie group): Let G be the group of affine transformations of R, x a x + b, a > 0. Exercise 3. Kalman filter continuous time: Example 1 Consider the system given by, \(\ddot{x} = u \), with measurement on position alone Kalman filter continuous time: Example 1 Consider the system given by, \(\ddot{x} = u \), with measurement on position alone. In this case, since the group is abelian, the Haar measure is both right and left Note that cr-finiteness is necessary, as the counting measure shows. Search: Cost Of Face Recognition Camera. A Radon measure is a Borel measure on a Hausdor lo-cally compact topological space which is nite on compact sets, inner and outer{regular on all open sets. com - *CHURCH SHOOTING* TWO DEAD = shooter KILLED Many Churches have a Safety Team MedStar Mobile Healthcare spokeswoman Macara Trusty told the Associated Press that two people were fatally shot at the West Freeway Church of Christ in White Settlement This is terrible T: 00 353 1 677 8099, E: [email protected] com on To see that (T 1A) = (A), let (A) = (g 1A), and note that is a Borel probability measure that is right invariant: for any h2H, Let m be the normalized Haar measure of a compact group G. For f C(G) or L1(G) show that m(f) = m(f) where the function f is dened as the function f(x) = f(x1). Search: Android Ble Example Github. The concrete examples described below provide a direct connection between the rather abstract theory of Haar measure and its application to situations which are relevan't in statistical applications. If we imagine the space of all pure states as a sphere, the Haar measure is equivalent to picking a random point on the sphere. It can also be proved that there exists an essentially unique right-translation-invariant Borel measure , but it need not coincide with the left-translation-invariant measure . For instance, a measure of one unit is given by the segment running from (1,1) to (e,1/e), where e is Euler's number. Example 5.. 14 (Haar Measure for ) For it turns out once again that quaternions come to the rescue. The standard Euclidean measure on Rnis the unique Haar measure on Rn for which the unit cube has measure 1. School Columbia University; Course Title ELECTRICAL elen; Type. The Haar measure is unique up to a scalar multiple. Therefore, the Lebesgue measure is a Haar measure normalized by \(\lambda \left ( \left [ 0,1\right ] ^{n}\right ) =1\). 13 Example 5 (Partly corresponds to Example C.5). Examples Random mixed qubits R H R P f(ph)d P(p)d H(h) de nes a left Haar measure on G. Solution. 2 Uniqueness of the Haar measure Theorem 2.1. I love React Native and have significant experience with it through a variety of apps SignalR with ASP Net Core SignalR is a framework from ASP NET Core allowing us to establish a two way communication between client and server Which of the single-page application libraries do you tend WebGL Water Another technique is to I am looking for examples of (not necessarily deep) results whose proofs rely on the Haar measure (or rather such that there exists an "elegant" proof involving it). Search: Kalman Filter Example Matlab Code. Check 'haar measure' translations into Tamil. Pages 512 Ratings 100% (1) 1 out of 1 people found this document helpful; This preview shows page 105 - 107 out of 512 pages. Section 9.2 contains a proof of the existence and uniqueness of Haar measure, and Section 9.3 contains additional basic properties of Haar measures. 'bures': The Bures measure. allowDuplicates - Boolean - [iOS only] allow duplicates in device scanning; scanningOptions - JSON - [Android only] after Android 5 BLE Device Activation 1 The Most Popular NVIDIA Linux News + Milestones Of 2020; Fedora Workstation 34 Looking To Employ Btrfs Zstd Transparent Compression By Default; Intel For the proof, we will use the example above of a measurable predicate. The Haar measure of the unit hyperbola is generated by the hyperbolic angle of segments on the hyperbola. For our purposes, a measure is a function which assigns a non-negative number to For discrete groups (groups with the discrete topology) the counting measure is a Haar measure. Convolution de mesures sur un groupe localement compact. Westra March 14, 2008 Abstract We give a way to nd the Haar measure on SU(2) 1 Introduction From some abstract mathematics we know that one a compact Lie group G there exists an up to scaling unique left-invariant integration measure d: Z G f(gh)d(h) = Z G f(h)d(h). Consider G= y x 0 1 jx;y2R;y>0 ; then one can check that up to a multiplicative constant,! i just want to know the gist of it, what is it rougly speaking, where can i apply it, how woul one apply it. The right Haar measure . Recall that a (left) Haar measure on a topological group is a (left-)translation invariant measure that is finite on compact sets and not everywhere zero. De ne the measure ~ as ~ ( A ) = ( A 1) where A 1 = f x 1 j x 2 A g for every subset A G . These measures are the same only for so-called unimodular groups (see below). Abstract. A measure with these properties is called Haar measure . Example 2. pokemon go pokemon coordinates list conic sections test UK edition a41 car accident; softway car wash; diesel barbershop stone oak; wireshark profiles repository; scummvm mt32 roms; phi psi syracuse; For an \(N\)-dimensional system, the Haar measure, often denoted by \(\mu_N\), tells us how to weight the elements of \(U(N)\). 2 Haar Measure 2.1 De nition Informally, the Haar measure is a uniform distribution over pure quantum states. [1] Haar measures are used in many parts of analysis and number Definition 6.1 ( Flner conditions) A sequence Fn of compact sets of positive Haar measure in an lcsc groupG is called. Thus, while E itself may not have i/-measure 0, almost every translate of E does. Search: Texas Ltc Test Questions And Answers. 2 Uniqueness of the Haar measure Theorem 2.1. For example, suppose \(f\) is a function that acts on elements of \(U(N)\), and we would like to take its integral over the group. An example of a non-unimodular group is the group of affine transformations. Face detection from the frames with the Viola jones Algorithm Create your face database for different classes with the detected regions (Faces) Apply them the sobel filter to see the only edges of the faces Extract the HOG features for all the processed sample in the database Face detection from live camera running more than Example of Kalman filtering Here is a simple example 01: see Generate Code for Online State Estimation in MATLAB I confirmed that the codes worked well in MATLAB 2013b One of the aspect of this optimality is that the Kalman filter incorporates all the information that can be provided to it But I really can't find a simple Hyperbolic angle has been exploited in mathematical physics with rapidity standing in for classical velocity. A left-invariant Haar measure is ( A) = A 1 a 2 d a d b, whereas a right-invariant Haar defined in ch. We identify an element x2GL d(R) with the vector containing its components (x 11;x 12;:::;x dd) 2Rd 2. Search: Human Face Generator Online. This measure is called the Haar measure. These ones compare the relevant information of the incoming image signal in real-time in photo or video in a database, being much more reliable and secure than the information Access authorization can be configured using a temperature detection threshold value in addition to the face recognition mode Mouse Then ~ is a right Haar measure on G . Example 13.4. A neighbourhood of x is an open set containing x. We introduce a version of Steins method for proving concentration and moment inequalities in problems with dependence. Search: Hilbert Huang Transform Python. Definition of Haar measure; Uniqueness. (Since is a 3D manifold, it may more appropriately be considered as a surface ``volume.'') The conditions are explained below: If are all measurable sets that are pairwise disjoint, and their union is , then is the sum of the values . If unit quaternions are used, recall that becomes parameterized in terms of , but opposite points are identified.It can be shown that the surface area on is the Haar measure. Let Hbe a subgroup of the compact topological group Gwhich is equipped with the Haar measure . 2 Haar Measure In this section we brie y introduce the notion of Haar measure and give a few examples. An example is given by the construction of Haar measure on a locally compact group. (eli5) i found nothing on youtube or reddit and the wiki page is to complicated. (Left-)Translation invariance means, that for all sets and elements we have . The additive group of a local eld Kis a locally compact group (it is a metric space, so it is automatically Hausdor ). A right Haar measure on G is defined similarly, except with left translation invariance replaced by right translation invariance ( (B g) = (B) for all sets B ). measure (i.e., a left Haar measure), u any Borel measure, andE any set of p-measure 0. Definition. The family HN (G) of Haar null subsets of a Polish group G is closed under translations, taking subsets and countable unions, see [THJ, 2.4.5]. Haar measure In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups.. x+A = \{x+a : a The question leaves your background a bit unclear, so I chat descriptively about the three Haar measures you are likely to be aware of without even A bi-invariant Haar measure is a Haar measure that is both left invariant and right invariant. The first few exercises in Section 5, Chapter XII of Lang's Real and Functional Analysis give formulas for Haar measure on some groups (exercise 9 is a nonabelian group). On a Lie group the Haar measure is given by f = G f , for all f C 0 G, where is the unique positive left invariant n form on G. For a Lie group G the modular function is given by g = det Ad g, for all g G. Examples ℝ, under addition. We will also require to be non-trivial: 6= 0 . measure on Gwith total measure 1. 3 Examples 20 4 Sources 22 1 Preliminaries: Topological groups, measures 1.1 Introduction In this project, we will explore the Haar measure, an important idea that establishes a notion of \volume" for many important topological groups. Example. One of the most useful properties of the Lebesgue measure is "translation invariance". ie. For any Borel set $A$, the measure of The guiding example to Haar measures is the Lebesgue measure on \(\mathbb {R}\) (or more generally on \(\mathbb {R}^{n}\)), which is invariant by left or right translations, as the group is abelian. c(G), h(x) = h(x1) for all x2G, and since V is symmetric,supp(h) V. Sincef;gandhareallcompactlysupported,hencesupportedonsetsofnite measure,Tonellistheoremappliesinthefollowingcalculations. smart goals examples for speech therapy; rails render partial on button click; harley oxygen sensor. A Haar measure is given by. Indeed, A Haar measure on a locally compact topological group Gis a) Let V be a compact neighborhood of 1 in G=H. Examples The Lebesgue measure on and is the Haar measure on the additive groups respectively. We'll cover face detection using Haar Cascade Classifiers using OpenCV Histogram of Oriented Gradients using Dlib How can we detect if a face is there or not ? if |G{H|8, or pHq 0 if |G{H| 8. Then Vei[/x] v(Et-x) = 0. A singleton has exactly then a Hair measure non-zero if the group is discrete. Integrals and the Haar Measure In this and the next chapter, background material on integration, topological groups and group actions is presented. If G=R\{0} under multiplication, then dx/|x| is the Haar measure (check!). Example 13.4. a right Haar measure. In most cases, to induce a measure on X = G / H you can simply pick a fundamental domain F G, and integrate over it (according to this, this can be done at least when G is -compact). One consequence, for example, that every finite-dimensional complex representation of a compact group is unitary with respect to a suitable scalar product.